
Introduction
Company valuation includes estimation of the cost of equity, which represents the risk of the cash flows. The most common method to estimate this risk is by using the Beta, which represents the relative risk of the analyzed company compared to the equity market.
Read Time: ~13 minutes
Content:
Beta description and use
Beta calculation
What Beta to use
Specific Risk Premium and Beta modification
Beta data sources
Beta Description and Use
First, a very short introduction to finance
Beta is part of the cost of equity calculation, so at first we need to understand the cost of equity, which itself is part of the cost of capital of the company (WACC) - so we will start from it. Every company or project that produces cash flows bears various risks, associated with those cash flows. The risks can be related to operations, market, regulation, exchange rates and so on. Those risks are usually called the asset risk. As part of an investment process investors are willing to receive a rate of return, which, in their opinion, compensates them for the risks associated with the projected cash flows. It may be a low rate of return for very stable projects, like rent from fully let residential buildings in high demand cities, or very high rates, like for hi-tech companies with no revenues. This rate of return is the cost of capital of the company itself. Often, companies divide their cash flow into several layers (I will not talk about the reasons for this in this article). Each layer has a different order of seniority. The most common separation is between debt and equity- we take a part of the projected cash flows and sell them as debt, and the remaining cash flows flow to the holders of equity. The distribution of cash flow between the different layers is called the cash flow waterfall:
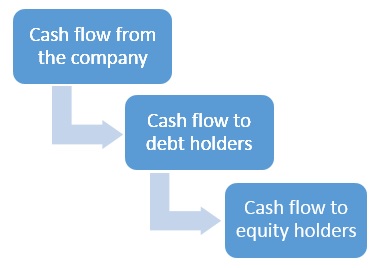
The risk of the debt holders not to receive their cash flows is lower than the risk of the equity due to their seniority, and of course depends on the portion of cash flows they are entitled to. As we can see, the cost of equity (rate of return to equity holders) for a company with no other layers should be equal to the cost of capital.
Since most companies have at least two layers (debt and equity) which are eligible to some part of the cash flows, it is hard to estimate the cost of capital directly. The popular method of estimation, is, therefore, indirect. By using market data we can estimate the cost of debt- the rate of return demanded by the debt holders, and the cost of equity- the rate of return demanded by the equity holders. Then, we calculate the weighted average to receive the cost of capital:
Cost of Capital = Cost of Equity * Weight of Equity + Cost of Debt * Weight of Debt * Tax Benefit Factor
The cost of debt is usually estimated by using the interest rate required by debt holders. This may be the yield to maturity of debentures issued by the company, or interest rate paid to bank loans.
And now we can talk about Beta
The cost of equity is estimated by using a formula which tends to calculate the rate of return, required by holders of the equity. This is executed by adjusting the average rate of return required by the investors in the whole equity market. In other words, the formula tends to estimate the relative risk of the cash flows to equity compared to the average risk in the equity market:
Cost of Equity = Risk Free Rate + Beta * Equity Market Premium
The equity market premium is the premium, required by the market over the risk free rate, for the holders of equity. As we can see, the Beta represents the ratio between the risks of the cash flows to equity of the company, compared to the average risk of the cash flows to equity holders of an equity market. The higher the Beta, the higher the relative risk, and vice versa.
As we have seen, the Beta is a representation of risk- in this context, the risk that future cash flows to equity would be different than the projected cash flows. The risks which the Beta represents can be divided to two- risks which stem from the risks of the cash flows of the company, and risks associated with the equity layer. The first group includes the risks we have talked about in the description of the cost of capital, the asset risks: operational, market, regulation, exchange rates and so on. The second is the risk associated with the equity layer - the financial risk, the risk created by leverage. It is caused by the seniority of other layers over the equity layer, which is the “last in line” to receive the cash flows of the company. For example, for a company which owns and rents an office building, we can think of several risks- over supply or low demand for office space in the area, unexpected roof leakage, increase in property tax, and so on. All those risks affect both cost of capital and cost of equity, it is the asset risk. The risk that does not affect the cost of capital, the financial risk, stems from the composition of the capital, the ratio between the different capital layers- debt and equity. The higher the portion of cash flows which need to serve the debt, the lower the cash flows left to the equity holders and the higher their risk.
For example, there are two similar companies with different capital compositions, the annual projected cash flow of each is 100$. Company A does not have a lot of debt and needs to pay 30$ to the debt holders each year, so 70$ is left to the equity holders. Company B is financed by a lot of debt and needs to pay 75$ to the debt holders each year, so 25$ are left to the equity holders. Now, one the market risks materializes and the demand of products in the industry declines a bit, so the cash flow of each company declines by 10$, a 10% decrease. The cash flow of equity holders of company A declines by those 10$ to 60$, a 14% decrease. The cash flow of equity holders in company B also declines by those 10$, to 15$, a 40% decrease:
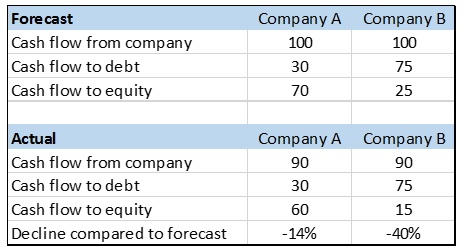
Since the risk of the cash flow to equity of company B is much higher compared to the risk of equity of company A, the Beta of company B should also be much higher compared to the Beta of company A. The Beta which expresses the total risk of cash flows to the equity holders is called “Levered Beta”, since it expresses the risk of the company and the risk of the leverage. The Beta which does not expresses the risk of the leverage is called the “Unlevered Beta”. Theoretically, the Unlevered Beta should express the risks of the company itself- the asset risks, represented by the cost of capital.
As we said before, Levered Beta represents the risk of the equity of the company compared to the risk of the equity market. Since it represents both the asset risks and the financial risk, we cannot deduce the source of risk just by the number itself. For example, a Beta of 1, similar to the risk of the market, can be influenced by multiple factors. This equity may by characterized by:
- Asset and financial risk similar to the average of the market.
- Higher asset risk and lower financial risk compared to the average in the market.
- Lower asset risk but higher financial risk compared to the average in the market.
If we want to understand the sources of risk represented by the Levered Beta, we need to calculate the Unlevered Beta, since it represents only the asset risk, and compare it to that of the market.
The main points of this section are:
- The risk of the cash flows of a company is represented by the rate of return required by the investors in the company, called the cost of capital.
- The cash flows of a company are usually divided between layers with different seniority, mostly between debt and equity.
- The risk of cash flows to equity are the same as the risks associated with the cash flows of the company, plus the leverage risk stemming from the low seniority of equity.
- The cost of equity is usually calculated by adjusting the return of an equity market to the risk of the equity layer of the specific company. The adjustment factor is called Beta.
- The Levered Beta is the ratio of the risk associated to the cash flows to equity of the company compared to the average risk of cash flows to an equity market.
- The Unlevered Beta expresses the risk of the company without accounting for the risk associated to the leverage.
Beta Calculation
Regression Beta
In the previous chapter, we defined the Levered Beta as the ratio of the risk associated to the cash flows to equity of the company, compared to the average risk of cash flows to an equity market. Since the return required by investors is directly linked to risks of the cash flows, we can estimate the Levered Beta by calculating the ratio between the rate of return of the equity to the rate of return of the market. This calculation is performed by estimating a linear regression where:
X- Rates of return of the market
Y- Rates of return of the equity of the company
By using this method we can only estimate the Levered Beta, since the returns we see in the market are the returns of the equity, expressing the risks of both the company and the leverage. To perform this regression analysis we need to input a series of returns of the equity of the company and a series of returns of an equity market, for the same period. Since we don’t have an estimation of future returns we must use historic returns, which raises several questions:
- What equity market to use?
Since we try to estimate the risk of the company by estimating its correlation with the risk of the market, we would like to use the returns of an equity market which is related to the risks of the company. Mostly, we will use the returns of the equity market in the same geography- for example, for a large U.K. company we will use the FTSE 100 index, but for a hi-tech company which operates in multiple markets we can use the NASDAQ index. We need to remember to use the same market for the calculation of the market risk premium in the cost of equity formula. If you are trying to decide between several possible equity markets, you can examine the R-squared of the regression output to determine the market to use. The higher the R-squared statistic, the higher the movement in the market explains the movement in the price of the company shares.
- What time period to use?
The choice of the time period to use is driven by two conflicting influences. On the one hand, the longer the period, the more samples we have, and more samples improve the quality of the regression. On the other hand, the most recent period should better resemble current, and probably future, market conditions. Since we try to forecast future risks (or returns), it is important to use a period which resembles expected market conditions. With this in mind, we will pick the longest period possible, usually up to 5 years. For example, if the environment in which the company operates was stable in the last 5 years, and expected to remain the same in the future, we can use 5 years of returns data. But, if the regulation in the company’s market changed drastically 2 years ago, it will be better to use data of the last 2 years.
- What time intervals to use?
We can use daily, weekly and even monthly and quarterly data. The problem with monthly data is that if we decided on a period of 1 year, we will have only 12 samples, or 4 samples for quarterly intervals. On the other hand, a very short time interval, such as daily, might include a lot of “noise”, since daily stock returns are considered pretty much random. Also, low liquidity, causing a low trading volume in the stock, can mislead since most of the daily price changes will be very low. This will imply low risk compared to the market, while the truth may be exactly the opposite.
The main thing to keep in mind is that we would want to use data which will be the best representative of the future.
Levered and Unlevered Beta
The difference between the Levered and Unlevered Beta is the financial risk, or the risk of leverage. Because of that, the estimation of the Unlevered Beta is performed by adjusting the Levered Beta (calculated by using the regression analysis method) to the leverage of the company. The most common formula used to perform this calculation is the Hamada equation, named after Robert Hamada:
Levered Beta = Unlevered Beta * [ 1 + ( 1 – Tax Rate ) * Debt / Equity ]
The equation transforms the Unlevered Beta to Levered Beta by multiplying the Unlevered Beta by the ratio of debt to equity, while also accounting for the tax benefit of the use of debt. Of course, the Hamada equation also enables calculating the Levered Beta with the Unlevered Beta as the input. For example, if we calculate the regression Beta of several companies in a specific industry, we can calculate the Unlevered Beta of each company and receive the average Unlevered Beta of the industry. This Unlevered Beta should represent the average asset risk of this group of peer companies. This make sense because often, companies in the same industry share similar risks, but different leverage. Then, we can estimate the Levered Beta of the analyzed company by adjusting the average Unlevered Beta of the industry to the leverage of the analyzed company by using the equation. Updated and historic Unlevered Beta data of various industries and geographies can be found in Damodaran’s website.
The input of the debt and equity numbers raises a question, which values to use- market values or book values? Usually, the market value of debt does not differ much from the book value, but the equity value might be very different. Also, the market value of equity might be different compared to the value we compute in the valuation. There are several arguments in favor of using each value:
- Market Value: The Hamada formula, and most other beta levering and delivering formulas, are based on measuring debt capital and equity capital at market values.
- Valuation Value: Since the cost of capital used in the valuation should be consistent with the input values used, the value of equity used in the formula should be the same as the value of equity in the valuation. Since the value of equity used changes the cost of capital and, accordingly, the value in the valuation, the application of this value requires applying “goal seek” iteration to the valuation. To perform this, input the equity value of the valuation to the cost of capital formula, this will probably change the value of equity- continue changing the value until both numbers are similar.
- Book Value: Many companies think of leverage in terms of book values, which are usually more stable compared to market values. Most companies define book value based leverage targets. Also, credit rating companies also refer to book values when determining leverage.
Other beta levering and delivering formulas, which I won’t discuss here, are: Miles-Ezzel formulas, Harris-Pringle formulas, practitioners’ method formulas and Fernandez formulas.
Beta Smoothing- Blume’s Method
Studies have found that single security Beta for a specific period were not a good predictors of the Beta in the following period, as extremely high and low Betas had a tendency to over and under predict. They also found that betas tend to gravitate toward the market beta of 1 in the long term. The solution to this phenomenon is Beta smoothing. This can be performed by using Blume’s method- multiplying the Beta by 2/3 and adding 1/3. This basically gives the calculated Beta a weight of 2/3, and the market Beta of 1 a weight of 1/3.
Beta Estimation- Using Analystix Tools
The Cost of Capital Calculator, part of the Analystix Tools Excel Add-ins package, Includes the Beta Calculator which allows you to easily calculate the Levered Beta of the company by using all the mentioned above methods:
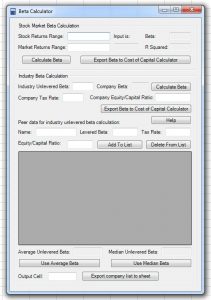
- The “Stock Market Beta Calculation” section allows you to calculate the regression Beta by selecting a series of stock and market prices or returns. It performs the regression analysis and exports the Levered Beta and the R-squared.
- The “Industry beta Calculation” section allows you to calculate the Levered Beta of a company using the Hamada equation. The required input is the average Unlevered Beta of the industry, the tax rate and the leverage of the company
- The “Peer data” section allows you to compute the Unlevered Betas of peer companies and use the average of median as input for the Unlevered Beta of the industry. The required input is Levered Betas, tax rates and leverage of peer companies.
Click here for the Beta Calculator Tutorial page.
What Beta to Use
We have seen 3 common methods of Beta estimation:
- Regression Beta
- Levering the average Unlevered Beta of the industry
- Levering the average Unlevered Beta of peer companies
The question is, in what circumstances it is best to use each of the methods? In the explanation of the regression Beta calculation we said that the main thing to keep in mind is that we would want to use data which will be the best representative of the future. The same applies to the choice of method for estimation- the method which will give us the best representative of the future is the one to use. Let’s look at the advantages and disadvantages of each method:
Regression Beta
The regression Beta of the company should, theoretically, provide the best representation of the risks of the company, as we use the market data of the company itself. The problem here is that markets are often not so efficient when it comes to specific stocks. A stock with low liquidity will experience periods with no changes in stock price which will make the calculation skewed, and of course we cannot use this method for private companies with no stock price data. Another potential problem with using the regression Beta is when the company experienced a recent change which affected its risk, so we would not have enough historic data samples to calculate the regression. In summary, the regression Beta will not be used if the analyst believes that the stock movements of the analyzed company are not a good representative of its risk relative to the market, or if he deduces that past characteristics of risk of the company have recently materially changed and would not represent future risk characteristics.
Industry Beta
The use of the Unlevered Beta of the industry solves some of the problems with using the regression Beta of the company. Since it is calculated by using the average regression Beta of many firms, the inefficiency of the market should be much lower compared to using sample of one company. Also, we can use this method for low liquidity and private companies.
The problem with a material change in the characteristics could be solved by this method, depending on the situation- if we think that future risk characteristics of the company are similar to those of other companies in the market in recent years, the use of industry Beta will be useful. On the other hand, if we think that the risk of the company is different compared to other companies in the industry, this method will not provide a representative Beta and we would need to modify it.
Peer companies Beta
The use of the average Unlevered Beta of company peers is close to using the Unlevered Beta of the industry, only in this method we choose the companies which will be used in the calculation. This method will be used when we don’t have an estimate of the Unlevered Industry Beta, or when we want to control for the companies which are included in the calculation. Analysts with a good acquaintance with companies in the industry can use a sample of companies with similar risk characteristics as the company analyzed.
Like before, the main thing to keep in mind is that we would want to use the method which will provide the best representative of the future.
Specific Risk Premium and Beta Modification
Sometimes we would use the industry or the peer companies’ methods, but will also consider them to be inferior representatives of the risk of the company. For example, when estimating the Beta of a private local company we might have to use a sample of Betas of companies of the same industry, but in a different country. Another example we used before is a recent change, like a new regulation, which will make the historic data a bad representative of the future. In this case, we would want to adjust the cost of equity to the specific situation. The most common method to do so is to add or subtract a specific risk premium- a risk premium which should account for the difference between the risk captured by the Beta we used in the equation and the “real” risk. Unfortunately, it is very hard to estimate an objective measure of the specific risk premium.
Another method, which can be used in a situation where the risk changed due to a change in the market, is to find a market or company which experienced a similar change in the past. Then, we can calculate the ratio between the Beta before and the Beta after this change. Then, we would apply this ratio on the Beta used in the cost of equity equation. So, in our previous example, if we find a market which experienced a similar change in regulation, and we compute and find that the Beta of this market changed from 0.7 to 0.9, we can multiply our Beta by the same ratio (0.9/0.7= 1.28).
The main thing to keep in mind then adding a specific risk premium or adjusting the Beta is that this modification stems from our assessment that the calculated Beta does not provide a good representation of the risk of the analyzed company.
Beta Data Sources
| Source | Website | Description |
|---|---|---|
| Damodaran | Link | Current and historic data of levered and unlevered beta for 94 industries and in 7 regions. Includes parameters used in the calculations. |
| Duff & Phelps | Link | Publishes annual Valuation Handbook which includes beta data for 180 U.S. industries and size groupings. |
| salvidio & partners | Link | Publishes Quarterly Industry Beta report, including levered and unlevered Beta for periods of 2 and 5 years for 134 industries and 10 regions. |

